2D Fundamentals

Overview

We treat the Purkinje network as a fractal tree. Each branch grows by adding short segments at its tip; the direction is steered by a repulsion field that keeps new points away from the already-built tree and preserves spacing. The page summarizes the growth rule used in the paper [1] and maps it to the library API.

Discrete growth rule

Let \(\mathbf{x}^i\) be the end point of the i-th segment of a branch and \(\mathbf{d}^i\) the unit direction of that segment. Growth proceeds by computing a new direction and then advancing a fixed step:

(1)\[\mathbf{d}^{\,i+1} \;=\; \frac{\mathbf{d}^{\,i} + w\,\nabla d_{\mathrm{CP}}(\mathbf{x}^i)} {\left\lVert \mathbf{d}^{\,i} + w\,\nabla d_{\mathrm{CP}}(\mathbf{x}^i)\right\rVert}, \qquad i>1,\]
(2)\[\mathbf{x}^{\,i+1} \;=\; \mathbf{x}^{\,i} + \frac{\ell_b}{N_s}\,\mathbf{d}^{\,i+1}.\]

Where

  • \(d_{\mathrm{CP}}(\mathbf{x})\) is the distance to the closest point already in the tree, and \(\nabla d_{\mathrm{CP}}\) points in a repulsive direction.

  • \(w\) is the repulsion weight controlling how strongly tips avoid existing branches.

  • \(\ell_b\) is the branch length for the current generation.

  • \(N_s\) is the number of segments per branch; the step size is \(\ell_b/N_s\).

Initial direction at bifurcation. When a new branch is spawned, its first direction \(\mathbf{d}^1\) is obtained by rotating the parent’s last direction by the branching angle \(\pm \alpha_b\) within the local tangent plane. For subsequent segments, use ((1))–((2)).

Parameter mapping (paper → library)

  • \(\ell_b\) → FractalTreeParameters.length (median branch length).

  • \(\alpha_b\) → FractalTreeParameters.branch_angle (branching angle).

  • \(w\) → FractalTreeParameters.w (repulsion weight).

  • \(N_s\) → implicit via the step length: FractalTreeParameters.l_segment controls the step; typically \(N_s \approx \lceil \ell_b / \texttt{l\_segment} \rceil\).

  • Segment spacing / collisions → Nodes.collision(), with KD-tree updates via Nodes.update_collision_tree().

Implementation notes

  • The direction update is renormalized every step (unit vector).

  • Multiple branches may grow “in parallel” (one step at each active tip) until the current generation reaches \(N_s\) segments.

  • The geometric update is performed in a parameter space (2D chart) and projected back to the endocardial surface; see Projection to the Heart Surface.

Figure

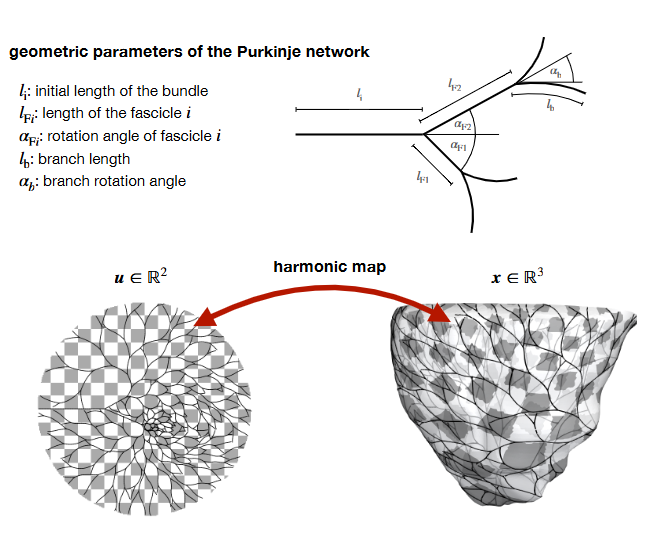
Schematic of branch extension and bifurcation (paper Figure 2)

Fig. 3 Paper schematic of the growth process, showing the role of \(\ell_b\), \(\alpha_b\), and \(w\). See [1] §2.1.

API cross-reference

  • purkinje_uv.fractal_tree_uv.FractalTree – orchestrates growth (grow_tree), maintains edges, connectivity, end_nodes.

  • purkinje_uv.branch.Branch – computes the next step and requests projection/collision checks.

  • purkinje_uv.mesh.Mesh – project_new_point, gradient, detect_boundary, compute_uvscaling (used during growth).

  • purkinje_uv.nodes.Nodes – spacing control: collision, update_collision_tree.

Algorithm flow (generation loop)

        flowchart TD
  A([Start]) --> B[FractalTree.grow_tree()]
  B --> C[Init nodes/edges and seeds]
  C --> D{More generations?}
  D -->|Yes| E{Active tips left?}
  D -->|No| Z[Finalize: build PurkinjeTree(nodes, connectivity, end_nodes)]

  E -->|Pick tip t| F[Branch.step()]
  F --> G[Update direction d_next = normalize(d + w * grad dCP)]
  G --> H[Propose 2D step: l_b / N_s]
  H --> I[Map 2D to 3D candidate]
  I --> J[Mesh.project_new_point(candidate) -> x_proj]
  J --> K{Nodes.collision(x_proj)?}

  K -->|Too close| L{Reduce step?}
  L -->|Yes| H
  L -->|No| M[Terminate tip; mark end node]
  M --> E

  K -->|OK| N[Append node and Edge(n_prev, new)]
  N --> O{Reached N_s segments this generation?}
  O -->|No| E
  O -->|Yes| P{Bifurcate here?}
  P -->|Yes| Q[Spawn child tips with +/- branch_angle]
  Q --> E
  P -->|No| E

  Z --> END([Done])

Fig. 4 Algorithm flow for the fractal-tree generation loop.

Single step: class interaction

        sequenceDiagram
  participant FT as FractalTree
  participant BR as Branch
  participant ME as Mesh
  participant NO as Nodes

  FT->>BR: step()
  BR->>BR: compute d_next (w · grad d_CP)
  BR->>ME: project_new_point(candidate)
  ME-->>BR: x_proj
  BR->>NO: collision(x_proj)
  NO-->>BR: ok / too close
  alt ok
    BR-->>FT: append node & Edge(n_prev, new)
  else too close
    BR-->>FT: reduce step or terminate tip
  end

Fig. 5 One growth step — who calls whom.

References

  • [1] — Section 2.1 (Purkinje network generation), Figure 2.