Projection to the Heart Surface

Summary

Instead of advancing branches directly on a curved 3D endocardial surface, we grow the network in a parameter space (a 2D plane or a locally flattened chart) and then project each new point back to the endocardium. This greatly improves robustness on highly curved or irregular meshes and keeps growth tangential to the surface.

Why not grow directly in 3D?

Direct 3D stepping tends to: - drift off-surface due to accumulated numeric error, - get trapped by highly acute triangles or noisy normals, - produce gaps in coverage on thin or tightly curved regions.

Projection pipeline

  1. Propose a 2D step Advance the branch tip in the parameter space using the 2D growth rule (see 2D Fundamentals for the discrete update).

  2. Map 2D → 3D candidate If a UV mesh is available, map the 2D point to an initial 3D candidate. Otherwise, use the last 3D tip and the proposed direction to form a small 3D offset.

  3. Pre-project along the vertex normal (optional but recommended) From the candidate point, move a short distance along the local vertex normal to reduce penetration or hovering.

  4. Snap to the surface Use a triangle locator (VTK cell locator / nearest‐triangle search) to project the point onto the closest triangle; clamp barycentric coordinates to ensure the point sits on the triangle and not outside its edges.

  5. Validate and accept - Enforce minimum spacing using purkinje_uv.nodes.Nodes.collision. - If the point violates spacing or leaves the manifold, reduce the step (l_segment) and retry. - On repeated failure, terminate the branch (creates an end node).

Implementation mapping

  • purkinje_uv.mesh.Mesh - project_new_point(candidate) – snaps a 3D candidate to the closest triangle. - gradient(p) – returns a surface gradient used to steer growth (tangent guidance). - detect_boundary() – marks boundary edges (useful for seeding/constraints). - compute_uvscaling() – builds/validates UVs and scaling for parameter‐space steps.

  • purkinje_uv.fractal_tree_uv.FractalTree - owns mesh (3D), optionally mesh_uv (2D chart), and the triangle locator, - calls grow_tree() which advances branches, projects new nodes, and appends edges.

  • purkinje_uv.branch.Branch - computes the next step in parameter space and requests surface projection, - consults purkinje_uv.nodes.Nodes for collision checks.

Robustness tips

  • Keep steps small: l_segment too large leads to overshoot on high curvature.

  • Use normals sparingly: a short pre-projection along the vertex normal reduces artifacts, but long moves can cross cavities on thin walls.

  • Rebuild collision tree: call Nodes.update_collision_tree() after batches of insertions.

  • Clamp UV steps: when using UV charts, prevent long jumps across seams.

Quality checks

  • Surface adherence: the dot product between triangle normal and the vector from the triangle plane to the new point should be ≈ 0 (within tolerance).

  • Coverage: compute the maximum distance from endocardial surface samples to the nearest network node; trend this metric while tuning FractalTreeparameters.

  • Degree sanity: endpoints must be degree-1 in the generated connectivity.

Minimal example

from purkinje_uv import FractalTreeParameters, Mesh, FractalTree

p = FractalTreeParameters()
mesh = Mesh.from_file("endocardium.vtu")
mesh.detect_boundary()
mesh.compute_uvscaling()  # optional if UVs are present

ft = FractalTree(mesh=mesh, params=p, mesh_uv=mesh)  # use a separate UV mesh if available
ft.grow_tree()  # projection happens internally

(Planned) figure

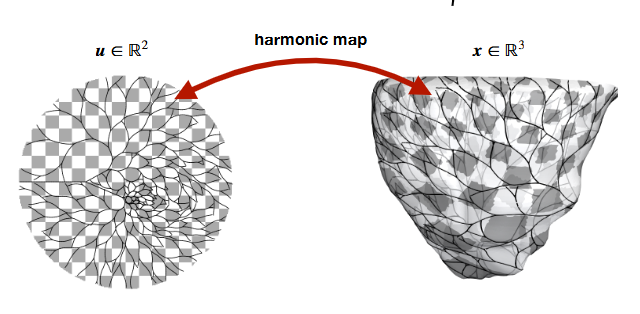
Two-step projection from parameter space to endocardial surface

Fig. 6 Schematic of the projection process: 2D growth → normal pre-projection → triangle snap.